슬라이딩 윈도우 기법 완벽 활용: 알고리즘 예시 및 문제 해결 방법

최근에, 나는 자료구조 및 알고리즘을 중심으로 코딩 문제를 연습하며 직장 변경을 준비하고 있었습니다.

이 과정에서 슬라이딩 윈도우 기법을 접하게 되었는데, 이 알고리즘이 매우 흥미로웠기에 커뮤니티와 나의 학습을 공유하고자 합니다.

이 튜토리얼은 competitive programming 인터뷰 준비에 유용할 것입니다. 그럼 시작해보겠습니다.

슬라이딩 윈도우 기법이란 무엇인가?

슬라이딩 윈도우 기법은 컴퓨터 과학과 신호 처리에서 사용되는 알고리즘 접근 방식으로, 더 큰 데이터 세트에서 고정 크기의 부분 집합, 또는 “윈도우”를 선택하고 이 윈도우를 단계적으로 데이터 세트를 통해 이동하는 것을 말합니다.

윈도우는 데이터 위를 슬라이드하며, 각 단계에서 윈도우 내의 요소들에 대한 어떤 연산을 수행합니다.

혼란스러우십니까? 이 기법을 예시로 좀 더 자세히 설명해보겠습니다.

슬라이딩 윈도우 예시

competitive programming 연습을 하고 있고 다음과 같은 문제를 마주친다고 가정해봅시다:

“O(N)의 시간 복잡도를 가진 크기 k의 서브 배열의 최대 합을 찾으세요.

Array = [1, 2, 6, 2, 4, 1], k = 3″

시간 복잡도 개념에 익숙하지 않다면, 여기 간단한 정의가 있습니다:

이론 컴퓨터 과학에서 시간 복잡도는 알고리즘을 실행하는 데 필요한 컴퓨터 시간의 양을 설명하는 계산 복잡도입니다.

및 그것에 대해 더 배우고 싶다면 여기에 코스가 있습니다.

우리의 문제로 돌아가서 본질적으로 우리가 해야 할 일은 합이 최대인(가장 큰 숫자) 크기 3의 서브 배열을 찾는 것입니다. 이를 해결하는 방법에 대한 시각적 뷰는 다음과 같습니다:

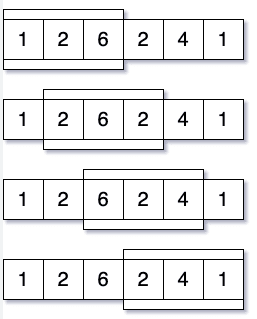
수동 해결
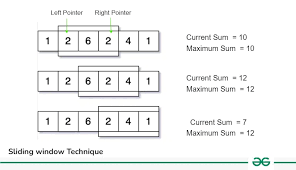
이제 수동으로 해결해봅시다. 위 이미지에서 크기 3의 각 서브 배열의 합을 찾아봅시다.

1번째 서브 배열의 합 = 1 + 2 + 6 = 9
2번째 서브 배열의 합 = 2 + 6 + 2 = 10
3번째 서브 배열의 합 = 6 + 2 + 4 = 12
4번째 서브 배열의 합 = 2 + 4 + 1 = 7
9, 10, 12, 7 중 최대(가장 큰) 숫자는 12 – 즉, 3번째 서브 배열입니다. 그것이 우리의 해결책입니다.

코드 해결

좋습니다, 이제 우리의 프로그래밍을 사용하여 이 문제를 해결해봅시다.

다음은 문제에 대한 나의 해결책입니다:

function findMaxSumOfSequence(listOfItems: number[], sequenceLength: number) {
  if (listOfItems.length < sequenceLength) {
    return null;
  }

  let maxSum = -Infinity;
  for (let i = 0; i <= listOfItems.length - sequenceLength; i++) {
    let sum = 0;
    for (let j = i; j < i + sequenceLength; j++) {
      sum += listOfItems[j];
    }
    maxSum = Math.max(maxSum, sum);
  }

  return maxSum;
}

const input = [1, 2, 6, 2, 4, 1],
  windowSize = 3;

console.log(
  `Maximum sum of a sub-array of window size ${windowSize} is ${findMaxSumOfSequence(
    input,
    windowSize
  )}`
);

이 위에 코드를 통한 빠른 이해를 위해.

나는 입력 배열 및 윈도우 사이즈를 아래에 정의하고, 이 파라미터들을 사용하여 findMaxSumOfSequence 메소드를 호출합니다.

입력 배열 크기가 윈도우 크기보다 크면 계산이 불가능하므로 null을 반환합니다.

최대 합을 음의 무한대로 가정합니다.

배열을 순회하며, 배열의 각 항목에 대해 다음 k 항목에 대해 순회하며 그 합을 찾고, 현재 윈도우 합이 기존 최대 합보다 크면 최대 합 변수에 현재 윈도우 합을 할당합니다. 마지막으로 최대 합을 반환합니다.

하지만, 문제는 여기서 끝나지 않습니다. 아주 주의 깊게 문제를 살펴보면, 우리는 O(N) 시간 복잡도로 해결책을 찾아야 합니다.

그래서, 위 해결책의 시간 복잡도가 어떻게 되는지 궁금하실 겁니다. 좋습니다, 위 해결책의 시간 복잡도는 O(N*k)입니다. 즉, 우리는 배열의 각 항목에 대해 k 번 반복하고 있습니다(중첩 for-loop).

O(N) 시간 복잡도는 주어진 배열을 단 한 번만 순회하여 최대값을 찾아야 함을 기본적으로 설명합니다.

슬라이딩 윈도우 기법 사용하기

한 번의 반복으로 이 문제를 어떻게 해결할까요? 여기에서 슬라이딩 윈도우 기법이 적용됩니다. 우리의 해결책의 시각적 표현을 다시 한 번 살펴봅시다:

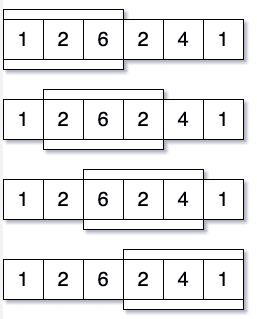
여기서, 윈도우가 배열 위를 슬라이드하는 것을 볼 수 있습니다. 초기에는 1번째 서브 배열에서 인덱스 0, 1, 2를 커버하고 있습니다. 다음 서브 배열을 위해, 오른쪽으로 한 위치를 슬라이드하여 왼쪽에 있는 0번 인덱스를 제거하고 오른쪽에 3번 인덱스를 추가합니다. 그래서 이제 2번째 서브 배열에서 1, 2, 3을 커버하게 됩니다… 그리고 이런 식으로 계속됩니다.

서브 배열에 대한 계산은 다음과 같은 방식으로 진행됩니다:

1번째 서브 배열 = 1 + 2 + 6 = 9
2번째 서브 배열 = 9 (1번째 서브 배열의 합) – 1 + 2 = 10
이를 주의 깊게 살펴봅시다. 우리는 1번째 서브 배열의 합이 9임을 찾았습니다. 2번째 서브 배열의 합을 계산하기 위해, 나가는 숫자(0번 인덱스에서의 1)를 빼고 들어오는 숫자(3번 인덱스에서의 2)를 더합니다.

3번째 서브 배열 = 10 (2번째 서브 배열의 합) – 2 + 4 = 12
4번째 서브 배열 = 12 (3번째 서브 배열의 합) – 6 + 1 = 7
이게 바로 슬라이딩 윈도우 기법입니다. 이 기법을 따르면, 단일 반복에서 최대 서브 배열의 합을 찾을 수 있습니다.

코드에서 슬라이딩 윈도우 구현하기

좋습니다, 다시 한 번 이를 구현해봅시다.

function findMaxSumOfSequence(listOfItems: number[], sequenceLength: number) {
  if (listOfItems.length < sequenceLength) {
    return null;
  }
  let start = 0,
    end = 0,
    maxSum = 0,
    windowSum = 0;
  while (end < sequenceLength) {
    windowSum += listOfItems[end];
    end++;
    maxSum = windowSum;
  }
  while (start + sequenceLength < listOfItems.length) {
    windowSum = windowSum - listOfItems[start] + listOfItems[end];
    maxSum = Math.max(windowSum, maxSum);
    start++;
    end++;
  }

  return maxSum;
}

const input = [1, 2, 6, 2, 4, 1],
  windowSize = 3;

console.log(
  `Maximum sum of a sub-array of window size ${windowSize} is ${findMaxSumOfSequence(
    input,
    windowSize
  )}`
);

위 코드를 이해해봅시다. 나는 findMaxSumOfSequence 메소드에 몇 가지 변경을 가했습니다. 윈도우 블록을 설명하는 start 및 end 변수를 도입했습니다.

이 구현에서는 2개의 루프가 있지만, 중첩되지는 않습니다. 이는 첫 번째 루프에서는 첫 번째 윈도우의 합을 찾아야 하고, 두 번째 루프는 첫 번째 루프의 결과에서 항목을 빼고 더하는 작업을 합니다.

위 예제에서, 첫 번째 루프는 첫 k 항목(3)인 1, 2, 6을 순회합니다. 나는 그 합을 계산하고 이를 maxSum 및 windowSum 변수에 저장합니다.

다음 루프에서, 나는 배열의 각 항목을 순회합니다. 각 항목에 대해 이전 번호를 빼고 다음 번호를 더하며, 이 결과를 windowSum 변수에 업데이트합니다. windowSum 및 maxSum 변수를 비교하고 windowSum이 더 크면 maxSum 변수를 업데이트합니다. 그런 다음 start 및 end 변수를 증가시켜 다음 서브 배열로 윈도우를 이동합니다. 마지막으로 최대 합을 반환합니다.

슬라이딩 윈도우 기법을 사용하여 크기 k의 서브 배열의 최대 합 찾기
이 구현으로 우리는 배열을 단 한 번만 순회하여 문제의 요구 사항을 만족시키며 O(N) 시간 복잡도로 서브 배열의 최대 합을 찾았습니다.

슬라이딩 윈도우 기법의 응용

슬라이딩 윈도우 기법은 다양한 분야에서 다재다능하게 활용됩니다.

• 배열 및 문자열 조작: 배열이나 문자열 처리에서, 슬라이딩 윈도우는 특정 조건을 만족하는 서브배열이나 서브스트링을 효율적으로 찾는 데 사용될 수 있습니다.
• 데이터 압축: 슬라이딩 윈도우 압축 알고리즘, LZ77 및 그 변형들은 입력 데이터에서 반복되는 패턴을 찾아 이전 발생에 대한 참조로 대체하는 데 윈도우를 사용합니다.
• 이미지 처리: 이미지 처리에서, 슬라이딩 윈도우는 특징 추출, 객체 검출 또는 이미지 분할 같은 작업에 사용될 수 있습니다.
• 신호 처리: 시계열 데이터는 슬라이딩 윈도우를 사용하여 로컬 패턴, 추세 또는 이상을 포착하는 데 분석될 수 있습니다.
• 네트워크 프로토콜: 슬라이딩 윈도우 프로토콜은 컴퓨터 네트워크에서 데이터의 신뢰성 있고 효율적인 전송을 위해 사용됩니다. 송신자와 수신자는 데이터 흐름을 관리하기 위해 허용 가능한 시퀀스 번호의 윈도우를 유지합니다.

결론

이 예시들을 통해 슬라이딩 윈도우 기법의 작동 방식을 명확하게 이해하셨기를 바랍니다. 이 기법을 사용하여 다른 문제를 해결해 보는 것이 익숙해지는 데 도움이 될 것입니다. 이 기법을 사용하여 크기 k의 서브 배열의 최소 합을 스스로 찾아보는 연습을 해보는 것이 유용할 것입니다.